SWAP Using CNOT is swapping memory without memory overhead.
Introduction
It is a standard exercise in quantum computing textbooks to construct a SWAP gate using CNOT gates as elementary building blocks.
Did you know that this construction is basically the classical algorithm we use all the time that swaps two memory locations without using any additional memory? I was talking to a few friends recently and was surprised they had never made this connection. So I’m writing this up.
SWAP and CNOT gates
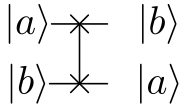
In quantum computing, a SWAP gate is used to swap the contents of two quantum registers. Its circuit diagram is as shown.
A CNOT gate, which is a controlled-NOT gate, applies the not gate to the second (target) qubit if the first (control) qubit is set to one. Its action is as follows.
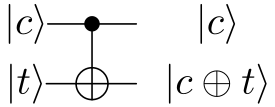
where \(\oplus\) is the classical XOR operation.
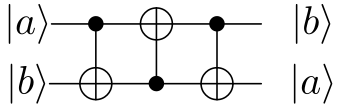
A SWAP gate can be constructed using 3 CNOT gates as follows.
Swapping two classical memory locations without using additional memory.
Given two memory locations \(a\) and \(b\), how do you swap their contents without using a third container? You can simply do the following,
a = a ^ b
b = b ^ a
a = a ^ b
where ^ is the classical XOR operation. You can verify that following this, the contents of \(a\) and \(b\) will be swapped.
They’re equivalent procedures
Now let’s write down what the SWAP gate circuit is doing mathematically.
\[\ket{a, b} \xmapsto{CNOT_{1, 2}} \ket{a, a \oplus b} \xmapsto{CNOT_{2, 1}} \ket{a \oplus (a \oplus b), a \oplus b} = \ket{ b, a \oplus b } \xmapsto{CNOT_{1, 2}} \ket{ b, (a \oplus b) \oplus b } = \ket{ b, a }\]Notice how these operations are the same as that in the code snippet above? That’s right.
Ciao!